В точном компьютерном и физическом моделировании нуждается любой инженер, особенно если компания хочет создать самый износостойкий и прочный подшипник, его свойства окружность и параметры должны быть известны, чуть ли не до уровня атома.
Представьте, вы даёте задачу программисту найти точный процент и модель соприкосновения подшипника, и оказывается что это невозможно, так как и невозможно смоделировать точную окружность. Как и невозможно смоделировать точную площадь соприкосновения.
Понятие круга является одним из универсальных математических понятий, дословно обобщаемым на случай произвольных метрических пространств. Но в разделе информатики, эта тема очень редко поднимается потому что до невозможности сложна.
Так что такое круг? И почему его точная математическая модель невозможна.

В научном понимании круг это правильный 65537 угольник (шестьдеся̀тпятьты̀сячпятисо̀ттридцатисемиуго́льник) — правильный многоугольник с 65 537 углами и 65 537 сторонами.
Насколько точны измерительные инструменты с Алиэкспресс? Выполняем поверку.
Значит для программиста круг это многоугольник с 65 537 углами — и эти углы будут соприкасаться с плоской поверхностью или такой же окружностью, и меняя равновесие всего это математического круга с 65 537 углами. Согласитесь что модель уже устарела?
Гауссом в 1796 году было доказано, что правильный n-угольник можно построить циркулем и линейкой, если нечётные простые делители n являются различными числами Ферма. В 1836 году П. Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует. Ныне это утверждение известно как теорема Гаусса — Ванцеля.
Могу даже открыть секрет настолько узкий в отрасли подшипников, что большинство автомобильных, железнодорожных и авиа катастроф происходит именно по причине некачественных подшипников так как проверить качество и окружность порой невозможно так как наука работает в основном не с числами а «диапазонами» то и процент брака в подшипниковой индустрии из-за проблемы создания идеально ровного подшипника самый высокий.
Такую проблему мы наблюдаем и в играх
Точность
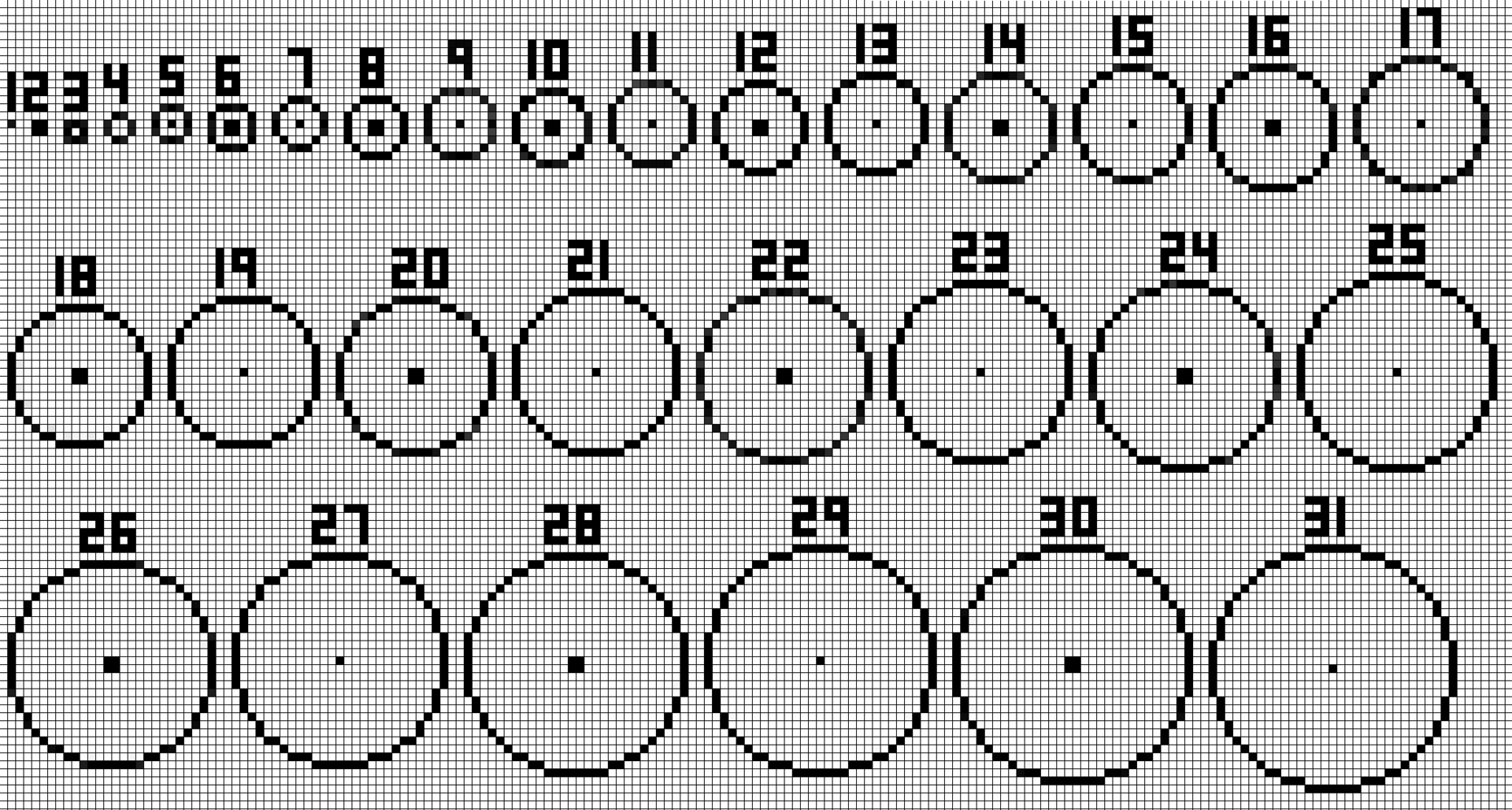
И эта точность очень низкая.
А 65 тысяч углов у круга это меньше миллиона.

Но даже и это не предел. Идеальный круг вообще бесконечен (имеет бесконечное количество углов). Как тогда его выразить в программировании, если любое число будет его неточной моделью? Или уже такая высокая точность будет ненужна? Ведь в любом массовом моделировании иза мельчайшей детали образуются каскадные лавинообразные эффекты которые дают разные результаты.
Спасибо за внимание.
Источник: habr.com
5 точнейших измерительных инструментов с Aliexpress
Сейчас в век высоких технологий рынок наводнили удивительные, точные, сплошь электрические и электронные инструменты и измерительные приборы. Неопытный или начинающий мастер подчас не в состоянии даже определить назначение того или иного предмета. Но тем не менее, старые добрые ручные инструменты и линейки будут нужны всегда!
Особенно качественные, точные, проверенные временем и одобренные профессионалами. И сегодня подборка именно непогрешимых ручных измерительных приспособ. Эти вещи будут полезны для тех, кто занимается изготовлением мебели и багетов для картин или ремонтом помещений — не для массовой продажи, для себя. Так же их можно порекомендовать людям, увлекающимся резьбой по дереву, моделированием.
Измерительный прибор от OOTDTY

Цена: от 901,83 руб. (проверить цену и скидку) Надёжность продавца: отличная!
Многозадачный измерительный инструмент позволяет не только проводить линейные измерения, но и находить центр окружности и проводить линии под заданым углом. Изготовлен из нержавеющей стали, разметка нанесена методом лазерной гравировки.
Классный центроискатель, углы точные, упаковано хорошо. Санька
Источник: best-stroy.ru
Правильный 65537-угольник
Правильный 65537-угольник (шестѝдесятипятиты̀сячпятисо̀ттридцатисемиуго́льник) — геометрическая фигура из группы правильных многоугольников, состоящая из 65537 углов и 65537 сторон. По причине малости центрального угла в графическом изображении правильный 65537-угольник почти не отличается от окружности (см. иллюстрацию справа).
Построение
Отличительная особенность 65537-угольника — это тот факт, что его возможно построить, используя только циркуль и линейку.
Число 65537 — это самое большое известное простое число Ферма:
 .
.
Гауссом в 1836 году было доказано, что правильный n-угольник можно построить циркулем и линейкой, если нечётные простые делители n являются различными числами Ферма. В 1836 П. Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует. Ныне это утверждение известно как теорема Гаусса — Ванцеля.
В 1894 же году Иоганн Густав Гермес после более чем десятилетних исследований нашёл способ построения правильного 65537-угольника и описал его в рукописи размером более 200 страниц [1] (оригинал рукописи хранится в библиотеке Гёттингенского университета).
Пропорции
Углы
 .
.
 .
.
Наглядное представление
Следующие соображения могут служить для иллюстрации пропорций практически не представимой фигуры:
- Отклонение центрального угла от 0°, а также отклонение внутреннего угла от 180° составляет всего лишь примерно 0,005°. Если приподнять за один конец лежащую на земле жердь длиной 104,3 метра только на один сантиметр, то она образует с землёй примерно этот угол.
Обоснование

Рассмотрим треугольник, одной стороной которого является указанная жердь, второй стороной — перпендикуляр, опущенный от приподнятого конца жерди на поверхность, где она лежала, а третьей стороной — отрезок от основания перпендикуляра до покоящегося конца жерди. Считая, что жердь подняли на один сантиметр, найдем какой длины она должна быть чтобы образовать с поверхностью угол , равный центральному углу правильного 65537-угольника: он будет равен отношению высоты, на которую подняли ли один край жерди к углу, который жердь образовала с поверхностью

- Если нарисовать 65537-угольник с длиной одной стороны 1 см, то его диаметр будет больше 200 м.
- Если нарисовать 65537-угольник с длиной одной стороны 1 м, то разница между радиусами его вписанной и описанной окружностей (диаметр каждой из которых будет около 10 км) составит всего лишь около 0,024 мм.
- Если нарисовать 65537-угольник диаметром 20 см, то длина одной его стороны окажется менее одной десятой толщины самого тонкого человеческого волоса.
Ссылки
- Правильные многоугольники
Wikimedia Foundation . 2010 .
- Мечеть Парижской Богоматери
- ДОКА Медиа
Полезное
Смотреть что такое «Правильный 65537-угольник» в других словарях:
- Правильный 17-угольник — Правильный семнадцатиугольник геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание 1… … Википедия
- Правильный 257-угольник — 257 угольник или окружность? Правильный 257 угольник правильный многоугольник с 257 сторонами. Содержание … Википедия
- Правильный многоугольник — Правильный семиугольник Правильный многоугольник это выпуклый многоугольник, у которого все стороны и углы равны . Определение правильного многоугольника может зависеть от определения … Википедия
- Правильный семиугольник — Правильный семиугольник это правильный многоугольник с семью сторонами. Содержание … Википедия
- Правильный шестиугольник — (гексагон) это правильный многоугольник с шестью сторонами … Википедия
- Правильный треугольник — Правильный треугольник. Правильный (или равносторонний) треугольник это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны … Википедия
- Правильный девятиугольник — это правильный многоугольник с девятью сторонами. Свойства Правиль … Википедия
- Правильный семнадцатиугольник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание … Википедия
- Правильный восьмиугольник — (октагон) геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов и все углы и стороны равны между собой … Википедия
- Правильный пятиугольник — Иное название этого понятия «Пентагон»; см. также другие значения. Правильный пятиугольник Правильный пятиугольник (греч … Википедия
- Обратная связь: Техподдержка, Реклама на сайте
- Путешествия
Экспорт словарей на сайты, сделанные на PHP,
WordPress, MODx.
- Пометить текст и поделитьсяИскать в этом же словареИскать синонимы
- Искать во всех словарях
- Искать в переводах
- Искать в ИнтернетеИскать в этой же категории
Источник: dic.academic.ru
